Seating Arrangement -Practice Problem from Hackerearth and solution using python 2.7.6

Problem Statement:

Akash and Vishal are quite fond of travelling. They mostly travel by railways. They were travelling in a train one day and they got interested in the seating arrangement of their compartment. The compartment looked something like 

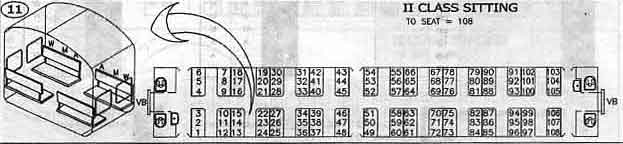
So they got interested to know the seat number facing them and the seat type facing them. The seats are denoted as follows : 

• Window Seat : WS
• Middle Seat : MS
• Aisle Seat : AS

You will be given a seat number, find out the seat number facing you and the seat type, i.e. WS, MS or AS.

INPUT
First line of input will consist of a single integer T denoting number of test-cases. Each test-case consists of a single integer N denoting the seat-number.

OUTPUT
For each test case, print the facing seat-number and the seat-type, separated by a single space in a new line.

CONSTRAINTS

• 1<=T<=10⁵
• 1<=N<=108

Programming using python 2.7.6:

From the problem statement and seating arrangement it depicts that in each row there are 12 seats (6 in each side) and which means there are two window seats(WS), 2 middle seats(MS) and 2 aisle seats(AS). 

Let's consider one row of seats and then it will be easy for us to get the solution.  

Window Seat : Seat number 1, 6, 7 and 12 are WS.

The person who is seating at Seat no 12 is opposite to Seat no. 1 and the difference from Seat no. 1 to Seat no 12 is 11, i.e n+11 (Where n is given seat number). Similarly seat no 1 is opposite to Seat no. 12 and the difference from seat no. 12 to seat no 1 is 11 i.e n-11 (Where n is given seat number).

In the same way Seat no 7 is opposite to Seat no. 6 and the difference from Seat no. 6 to Seat no 7 is 1, i.e n+1 (Where n is given seat number) and Seat no 6 is opposite to Seat no. 7 and the difference from Seat no. 7 to Seat no 6 is 1, i.e n-1 (Where n is given seat number).

Middle Seat : Seat number 2, 5, 7 and 11 are MS.

The person who is seating at seat no 11 is opposite to Seat no. 2 and the difference from Seat no. 2 to Seat no 11 is 9, i.e n+9 (Where n is given seat number). Similarly Seat no 2 is opposite to Seat no. 11 and the difference from Seat no. 11 to Seat no 2 is 9 i.e n-9 (Where n is given seat number).

In the same way Seat no 8 is opposite to Seat no. 5 and the difference from Seat no. 5 to Seat no 5 is 3, i.e n+3 (Where n is given seat number) and Seat no 5 is opposite to Seat no. 8 and the difference from Seat no. 8 to Seat no 5 is 3, i.e n-3 (Where n is given seat number).

Aisle Seat : Seat number 3, 4, 9 and 10 are AS.

The person who is seating at seat no 10 is opposite to Seat no. 3 and the difference from Seat no. 3 to Seat no 10 is 9, i.e n+7 (Where n is given seat number). Similarly Seat no 10 is opposite to Seat no. 3 and the difference from Seat no. 10 to Seat no 3 is 7 i.e n-7 (Where n is given seat number).

In the same way Seat no 9 is opposite to Seat no. 4 and the difference from Seat no. 4 to Seat no 9 is 5, i.e n+5 (Where n is given seat number) and Seat no 4 is opposite to Seat no. 9 and the difference from Seat no. 9 to Seat no 4 is 5, i.e n-5 (Where n is given seat number).

Let's only consider Seat number 1 to 12 , 

There are total 12 seats and you divide your seat number by 12 , below will be your outcome:

If remainder is 1 then it's a WS and  n+11 is the opposite person i.e. Seat number 12

If remainder is 2 then it's a MS and n+9 is the opposite person i.e. Seat number 11

If remainder is 3 then it's a AS and n+7 is the opposite person i.e. Seat number 10

In generic 

if remainder is 0,1,6 and 7 then it's a WS

if remainder is 2,5,8 and 11 then it's MS

if remainder is 3,4,9 and 10 the it's AS

This can be coded using if..elif statement, since python does not support switch case.

Code in Python 2.7 :

NumberOfTestCases = int(raw_input())

SeatNumber = list()

rem = 0

while NumberOfTestCases:

    SeatNumber.append(int(raw_input()))

    NumberOfTestCases -=1

for i in range(len(SeatNumber)):

    rem = SeatNumber[i]%12

    if rem == 1: #Window Seat

        print '{0} {1}'.format(SeatNumber[i]+11,'WS')

    elif rem == 2: #Middle Seat

        print '{0} {1}'.format(SeatNumber[i]+9,'MS')

    elif rem == 3: #Aisle Seat

        print '{0} {1}'.format(SeatNumber[i]+7,'AS')

    elif rem == 4: #Aisle Seat

        print '{0} {1}'.format(SeatNumber[i]+5,'AS')

    elif rem == 5: #Middle Seat

        print '{0} {1}'.format(SeatNumber[i]+3,'MS')

    elif rem == 6: #Window Seat

        print '{0} {1}'.format(SeatNumber[i]+1,'WS')

    elif rem == 7: #Window Seat

        print '{0} {1}'.format(SeatNumber[i]-1,'WS')

    elif rem == 8: # Middle Seat

        print '{0} {1}'.format(SeatNumber[i]-3,'MS')

    elif rem == 9: #Aisle Seat

        print '{0} {1}'.format(SeatNumber[i]-5,'AS')

    elif rem == 10: #Aisle Seat

        print '{0} {1}'.format(SeatNumber[i]-7,'AS')

    elif rem == 11: #Middle Seat

        print '{0} {1}'.format(SeatNumber[i]-9,'MS')

    elif rem == 0: #Window Seat

        print '{0} {1}'.format(SeatNumber[i]-11,'WS')

   

    rem = 0

Magical Word - Practice Problem from Hacker Earth and solution using python 2.7.6

Problem Statement: Dhananjay has recently learned about ASCII values. He is very fond of experimenting. With his knowledge of ASCII values and character he has developed a special word and named it Dhananjay's Magical word.

A word which consist of alphabets whose ASCII values is a prime number is a Dhananjay's Magical word. An alphabet is Dhananjay's Magical alphabet if its ASCII value is prime.

Dhananjay's nature is to boast about the things he know or have learnt about. So just to defame his friends he gives few string to his friends and ask them to convert it to Dhananjay's Magical word. None of his friends would like to get insulted. Help them to convert the given strings to Dhananjay's Magical Word.

Rules for converting:

1.Each character should be replaced by the nearest Dhananjay's Magical alphabet.

2.If the character is equidistant with 2 Magical alphabets. The one with lower ASCII value will be considered as its replacement.

Input format:

First line of input contains an integer T number of test cases. Each test case contains an integer N (denoting the length of the string) and a string S.

Output Format:

For each test case, print Dhananjay's Magical Word in a new line.

Constraints:

1 <= T <= 100

1 <= |S| <= 500

Programming using Python 2.7.6: I solved Dhananjay's Magical Word using python 2.7.6 and below is my code. However before looking in to code you must understand the problem statement:

If you go through the problem statement, it clearly articulated that input format as string - which means user can input any string (e.g. special character, alphanumeric, mix of small and capital alphabet etc). For character (whether it's a numeric, special character or small or capital alphabet) within a given string should be replaced only by nearest alphabet whose ASCII value should be prime (Dhananjay's Magical Number). Again if the character is equidistant to two prime ASCII value of alphabet (Dhananjay's Magical Number) then lower ASCII value should be taken.

Code in Python 2.7: 

Alphabet = ['A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z','a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z']

FinalPrimeAlphaASCII = []

#num = int(raw_input())

def isprimenumber(number):

    flag = 0

    for i in range(2,number/2 +1):

        if number % i == 0:

            flag = 1

            break

    if flag == 0:

        return True

for Alpha in Alphabet:

    if isprimenumber(ord(Alpha)): FinalPrimeAlphaASCII.append(ord(Alpha))

magicalword = ''

magicalwords = []  

NumberOfTestCases = int(raw_input())

while (NumberOfTestCases > 0):

    N = int(raw_input())

    userinput = raw_input()

    for s in userinput: # Iterate through each character in given string         

        if ord(s) <= FinalPrimeAlphaASCII[0]: # Any character whose ASCI value less than or equal to 67

            magicalword = magicalword + chr(FinalPrimeAlphaASCII[0])

        elif ord(s) >= FinalPrimeAlphaASCII[len(FinalPrimeAlphaASCII)-1]: # Any character whose ASCI value greater than or equal to 89

            magicalword = magicalword + chr(FinalPrimeAlphaASCII[len(FinalPrimeAlphaASCII)-1])

        elif ord(s) in FinalPrimeAlphaASCII: # Any character whose ASCII value is prime number

            magicalword += s

        else:

            i = 1

            while i < len(FinalPrimeAlphaASCII):

                #print ord(s)

                if ord(s) < FinalPrimeAlphaASCII[i]:

                    #If the character is equi-distant with 2 Magical alphabets.

                    #The one with lower ASCII value will be considered as its replacement

                    if (ord(s) - FinalPrimeAlphaASCII[i-1]) == (FinalPrimeAlphaASCII[i]-ord(s)):

                        magicalword +=chr(FinalPrimeAlphaASCII[i-1])

                        break

                    elif (FinalPrimeAlphaASCII[i]-ord(s)) < (ord(s) - FinalPrimeAlphaASCII[i-1]):

                        magicalword +=chr(FinalPrimeAlphaASCII[i])

                        break

                    else:

                        #Each character should be replaced by the nearest Dhananjay's Magical alphabet.

                        magicalword +=chr(FinalPrimeAlphaASCII[i-1])

                        break

                i +=1

       

           

    magicalwords.append(magicalword)

    magicalword = ''

    NumberOfTestCases -=1

   

for word in magicalwords: print word